Satz des Pythagoras

Satz: In einem rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat.

Bemerkung: Werden die Katheten, also die Dreiecksseiten am rechten Winkel, mit $a$ und $b$ und die Hypotenuse, also die Dreiecksseite gegenüber dem rechten Winkel, mit $c$ bezeichnet, so kann man den Satz des Pythagoras in die folgende Gleichung übersetzen: $a^2 + b^2 = c^2$

Beweis: Im folgenden werden mit der Zeit verschiedene Beweise für den Satz des Pythagoras aufgenommen, den Anfang macht der Beweis nach Euklid.

_{Quelle: §47 (L.33) im ersten Buch der Elemente}

ABC sei ein rechtwinkliges Dreieck mit dem rechten Winkel an A ($\angle CAB = \alpha$). Zu zeigen ist dann: $a^2 = b^2 + c^2$.

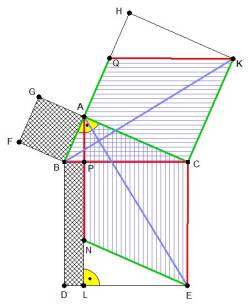
Man zeichne über a das Quadrat BDEC, über b das Quadrat ACKH und über c das Quadrat BAGF. Dann zeichne man durch A eine Senkrechte auf DE (Schnittpunkt: L) und zeichne die Strecken AD und FC ein. Man erhält dann Bild1.

Da die Winkel BAC, BAG und CAH nach Konstruktion rechte Winkel sind, sind die Strecken CG und BH also jeweils Geradenabschnitte.

Die Winkel FBA und CBD sind nach Konstruktion ebenfalls rechte Winkel und liegen beide am Winkel ABC des Dreiecks. Daher sind die Winkel FBC = FBA + ABC und ABD = ABC + CBD gleich groß. Da außerdem die die Längen der Strecken AB und FB bzw. CB und BD übereinstimmen, sind die Dreiecke nach dem Kongruenzsatz SWS¹⁾ kongruent. Damit sind also auch die Strecken AD und FC gleich lang (s. Bild 2).

Im nächsten Schritt ergänzt man nun die Teildreiecke FBC und ABD zu Parallelogrammen (Bild 3, die Färbung der Quadrate wurde der Übersicht halber entfernt). Diese Parallelogrammen haben den doppelten Flächeninhalt der Dreiecke und sind, da die Dreiecke kongruent sind, ebenfalls gleich groß. Jetzt kann man den Scherungssatz²⁾) anwenden:

Das Parallelogramm FBCM und das Quadrat FBAG liegen zwischen den parallelen Geraden durch FB bzw. CG. Daher ist ihre Höhe gleich groß. Da außerdem die Länge der Strecke CM gleich der Länge der Strecke AG ist, ist der Flächeninhalt des Paralleogramms FBCM gleich dem Flächeninhalt des Quadrates FBAG.

Das Parallelogramm ABDN und das Rechteck BDLP liegen zwischen den parallelen Geraden durch DB bzw. LA. Daher ist ihre Höhe gleich groß. Da außerdem beide die Strecke BD als Grundlinie haben, ist der Flächeninhalt des Parallelogramms ABDN gleich dem Flächeninhalt des Rechtecks BDLP.

Im Beweis wurde gezeigt, dass die Parallelogramme FBCM und ABDN gleichen Flächeninhalt haben. Daher haben also auch das Quadrat FBAG und das Rechteck BDLP gleichen Flächeninhalt (s. Bild 4).

Ebenso kann man zeigen, dass das Quadrat ACKH und das Rechteck LECP flächengleich sind.

Damit ist der Satz bewiesen.