Inhaltsverzeichnis
Anwendungsaufgaben mit Matrizen
Zwei Beispiele: Populationsentwicklung bei Kaninchen (Fibonacci) sowie eine Bevölkerungsentwicklungsaufgabe.
Alle Aufgaben dieses Typs fangen mit einer Startpopulation an und entwickeln sich im Laufe der Zeit - die Population nach einer gegebenen Zeiteinheit erhält man dabei immer durch Multiplikation des Startvektors mit der Entwicklungsmatrix. Die Untersuchung der Populationsentwicklung hat dann zum Ziel, die Entwicklung über einen längeren Zeitraum zu beschreiben - ob die Population wächst, stabil ist (also gleich bleibt) oder abnimmt.
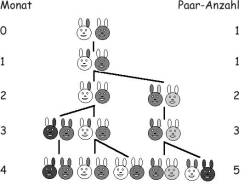
Kaninchenpopulation - Fibonacci
| Zeitpunkt: | am Anfang | nach 1 Monat | nach 2 Monaten | nach 3 Monaten | … | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … | 40 | … | n+1 |
| Kaninchenpaare x: | x0 = 1 | x1 = 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | … | x39+x38 | … | xn+xn-1 |
| davon geschlechtsreif: | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | … | |||
Annahme: Ein Kaninchenpaar benötigt einen Monat bis zur Geschlechtsreife, ab dann wird monatlich ein Paar Junge geworfen. Außerdem soll davon ausgegangen werden, dass keine Kaninchen sterben.
Rekursiv, also immer auf die schon ermittelten Paar-Zahlen, lässt sich dann jede weitere Zahl der Folge aus der Summe der beiden vorhergehenden ermitteln. Da für die Formel immer zwei Vorgänger bekannt sein müssen, müssen hier auch zwei Startwerte, x0 = 1 und x1 = 1 angegeben werden. Die Rekursions-Formel lautet dann xn+1 = xn+xn-1. Die Zeitvariable n muss dann mindestens den Wert 1 haben, da der kleinste bekannte Wert x0 ist.
Durch die rekursive Angabe müssten für jeden neu zu ermittelnden Wert alle Vorgänger bekannt sein oder ermittelt werden - bei größerem n wird das dann schon recht aufwändig. Daher war man schon früh auf der Suche nach einer Formel, mit der man die einzelnen Glieder der Fibonacci-Folge direkt ausrechnen kann.
Aus der Matrizenrechnung ergibt sich der folgende Zusammenhang:
Das kann man leicht durch nachrechnen überprüfen:
denn
,
, usw.
Hier gilt ja auch , also
und
, also
, usw.
Führt man das gedanklich immer weiter, erhält man als Formel für das n-te Glied der Fibonacci-Folge
für
.
Hat man Derive (o.ä.), so kann man die n-te Potenz der Matrix leicht berechnen - von Hand müsste man immer noch alle Matrizenpotenzen nacheinander ausrechnen, wäre also nicht viel weiter als bei der rekursiven Formel.
Aus Überlegungen zum Goldenen Schnitt (einem Wert, dem sich das Verhältnis xn+1/xn annähert) erhält man Ausdrücke, die Terme der Art enthalten. Nach einigen Berechnungen erhält man dann schließlich eine Formel, mit der man jedes Folgenglied direkt ausrechnen kann:
Der gesuchte Wert für x40 lässt sich damit schnell berechnen: x40 = 165 580 141 
Beispiel einer Bevölkerungsentwicklung
Eine Population sei in drei Altersgruppen eingeteilt, die Jüngere (J), die Mittlere (M) und die Ältere (A). Die Entwicklung der Population wird in längeren Zeitabschnitten beobachtet (hier: 1/3 der max. Lebenszeit), d.h. nach einem Zeitabschnitt sind die noch lebenden Jüngeren zu Mittleren geworden und die noch lebenden Mittleren zu Älteren. Durch den vergleichsweise langen Zeitabschnitt kann man davon ausgehen, dass alle Älteren in einem Zeitabschnitt sterben.
Die neue Generation der Jüngeren ergibt sich aus der Summe der Geburten aller drei Vorgängergenerationen (wobei die Geburtenrate bei den Mittleren am größten sein sollte).
Diese Angaben lassen sich sowohl in einer Tabelle als auch in einem Übergangsdiagramm festhalten:
| Jt | Mt | JA | |
|---|---|---|---|
| Jt+1 | g1 | g2 | g3 |
| Mt+1 | 1 - s1 | 0 | 0 |
| At+1 | 0 | 1 - s2 | 0 |
Die jeweils nächste Generation (Jt+1, Mt+1, At+1) lässt sich also wie folgt berechnen:
Beispiel: J0 = 4000, M0 = 9000, A0 = 5000, g1 = 0,35, g2 = 0,6, g3 = 0,05, s1 = 0,1 und s2 = 0,3.
Damit ergeben sich für die ersten vier Generationen folgende Werte (Bn bezeichnet dabei den Bevölkerungsvektor zur jeweiligen Zeiteinheit, M die sich aus der Tabelle ergebende Matrix):
| t = | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Rechnung: | M*B0 | M*B1 = M2*B0 | M*B2 = M3*B0 | M*B3 = M4*B0 | |
| Jt | 4000 | 7050 | 4942 | 5662 | 4873 |
| Mt | 9000 | 3600 | 6345 | 4448 | 5096 |
| At | 5000 | 6300 | 2520 | 4441 | 3113 |
| Gesamtbevölkerung: | 18000 | 16950 | 13807 | 14551 | 13082 |
In diesem Beispiel sieht man, dass die Gesamtbevölkerung im Laufe der Zeit abnimmt - bei unveränderten Bedingungen wird diese Population mit der Zeit aussterben.
Würde man z.B. g1 leicht erhöhen, auf g1 = 0,4285, so erhielte man eine stabile Population.
Bei noch größeren Geburtenraten in allen drei Alterstufen müsste die Gesamtbevölkerung langfristig wachsen.