[[schule:ma:regelns2:lag:abstand]]
Zuletzt angesehen: • abstand
Zeige Quelltext
AdminLetzte ÄnderungenÜbersicht

Inhaltsverzeichnis

Übersicht Abstandsberechnung

Lehrbuch: Schroedel, Elemente der Mathematik 12/13, Grundkurs NRW, 2000

  • Abstand Punkt – Punkt (oder auch „Länge eines Vektors“) 1)
  • Abstand Punkt – Gerade 2)
  • Abstand Gerade – Gerade 3)
    1. Fall: sich schneidende Geraden
    2. Fall: parallele Geraden
    3. Fall: windschiefe Geraden

Abstand Punkt-Punkt

Pythagoras lässt grüßen - egal, ob die Punkte nun 2, 3 oder beliebig viele Koordinaten hätten.

d ~=~ sqrt{(x_1 -~ x_2)^2 + (y_1 -~ y_2)^2 }~~~~~~ oder

~~~~~~~d ~=~ sqrt{(x_1 -~ x_2)^2 + (y_1 -~ y_2)^2 + (z_1 -~ z_2)^2 }~~~~~~~~ oder …

Abstand Punkt-Gerade

Der Abstand zweier Objekte ist die Länge der kürzesten Verbindungsstrecke zwischen den beiden Objekten. Gesucht ist also der Schnittpunkt eines vom gegebenen Punkt ausgehenden Normalenvektors der Geraden mit der Geraden. Dann kann der Abstand zwischen diesen beiden Punkten berechnet werden.

Abstand Gerade-Gerade

1. Fall: sich schneidende Geraden

Der Abstand bei sich schneidenden Geraden beträgt immer 0 (im Schnittpunkt 8-)).

2. Fall: parallele Geraden

Der Abstand ist immer gleichbleibend, daher wählt man sich einen Punkt auf der einen Geraden (z.B. den Stützvektor) und berechnet dann den Abstand dieses Punktes zur anderen Gerade wie bei „Abstand Punkt-Gerade“.

3. Fall: windschiefe Geraden

Windschiefe Geraden sind nicht parallel, schneiden sich aber auch nicht (können also in der Ebene nicht vorkommen). Hier müssen also auf den Geraden die Punkte gefunden werden, deren Abstand minimal ist.

Beispielrechnung für windschiefe Geraden

Vorstellung

Man drehe die Geraden so, dass der Eindruck erweckt wird, dass sich diese Geraden schneiden.4) Gesucht ist jetzt derjenige Vektor, der senkrecht von der oberen Geraden auf die untere zeigt (in der entsprechenden Projektion also nicht zu sehen ist).

Eigenschaften des Vektors

  • Ein Fußpunkt liegt auf der einen Geraden.
  • Der andere Fußpunkt liegt auf der zweiten Geraden.
  • Der Vektor zwischen diesen beiden Punkten steht auf beiden Geraden senkrecht.

Beispielaufgabe

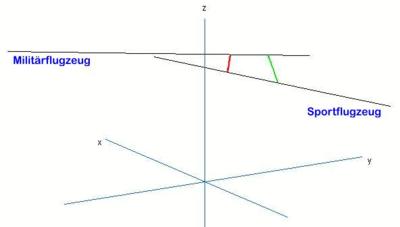
Zwei Flugrouten sollen als Geradengleichungen angegeben werden und ihr Abstand soll berechnet werden.5)

Geradengleichungen der Flugrouten

Ort zum Zeitpunkt 0: Stützvektor, Geschwindigkeitsvektor: Richtungsvektor

Sportflugzeug: ~~~s:~ vec{x} ~=~ vec{a} ~+~ lambda vec{v}~~~~~ also ~~~~~s:~ vec{x} ~=~ (matrix{3}{1}{0 4 2}) ~+~ lambda (matrix{3}{1}{200 {-100} 0})

Militärflugzeug: ~~~m:~ vec{x} ~=~ vec{b} ~+~ mu vec{w}~~~~~ also ~~~~~m:~ vec{x} ~=~ (matrix{3}{1}{3 0 3}) ~+~ mu (matrix{3}{1}{0 500 {-100}})

Fußpunkte P (auf s) und Q (auf m)

Da P auf s liegen soll und Q auf m, muss man für die jeweiligen Ortsvektoren nur die Geradengleichungen von s und m nehmen und anstelle des Vektors vec{x} die Vektoren vec{p} bzw. vec{q} verwenden:

vec{p} ~=~ (matrix{3}{1}{0 4 2}) ~+~ lambda (matrix{3}{1}{200 {-100} 0})~~~~~ und ~~~~~vec{q} ~=~ (matrix{3}{1}{3 0 3}) ~+~ mu (matrix{3}{1}{0 500 {-100}})

Der Verbindungsvektor PQ

Am Ende der Rechnung interessiert uns die Länge dieses Verbindungsvektors, daher ist es eigentlich egal, ob der Vektor vec{PQ} =~ vec{q} - vec{p} oder der Vektor vec{QP} = ~vec{p} -~ vec{q} betrachtet wird… Bleiben wir bei vec{PQ}.

vec{PQ} ~=~ vec{q} ~-~ vec{p} ~=~ [(matrix{3}{1}{3 0 3}) ~+~ mu (matrix{3}{1}{0 500 {-100}})] ~-~ [(matrix{3}{1}{0 4 2}) ~+~ lambda (matrix{3}{1}{200 {-100} 0})]

~~~~=~ (matrix{3}{1}{3 {-4} 1}) ~+~ mu (matrix{3}{1}{0 500 {-100}})~-~lambda (matrix{3}{1}{200 {-100} 0}) ~=~ (matrix{3}{1}{{3 - 200 lambda} {-4 + 500 mu + 100 lambda} {1 - 100 mu}})

Eigenschaften des Verbindungsvektors

Da der Vektor vec{PQ} auf beiden Geraden senkrecht stehen soll, muss das Skalarprodukt des Vektors mit den jeweiligen Richtungsvektoren 0 ergeben.

(matrix{3}{1}{{3 - 200 lambda} {-4 + 500 mu + 100 lambda} {1 - 100 mu}})~circ~(matrix{3}{1}{200 {-100} 0})~=~0~~~ und ~~~(matrix{3}{1}{{3 - 200 lambda} {-4 + 500 mu + 100 lambda} {1 - 100 mu}})~circ~(matrix{3}{1}{0 500 {-100}})~=~0

doubleleftright ~~~ 600 - 40000 lambda + 400 - 50000 mu - 10000 lambda ~=~0~~~~~ und ~~~~~-2000 + 250000 mu + 50000 lambda - 100 + 10000 mu ~=~ 0

doubleleftright ~~~ 1000 - 50000 lambda - 50000 mu ~=~ 0 ~~~~~ und ~~~~~-2100 + 260000 mu + 50000 lambda ~=~ 0

Lösen des Gleichungssystems

~~~~~~~ 1000 - 50000 lambda - 50000 mu ~=~ 0

wedge~~~~-2100 + 260000 mu + 50000 lambda ~=~ 0 ~~~|~~ addieren

doubleleftright ~~~-1100 + 210000 mu ~=~ 0

doubleleftright ~~~ mu ~=~ 11/2100 approx~ 0,0052

einsetzen: ~~~~~ lambda ~=~ 31/2100 approx~ 0,0148

lambda und mu in vec{PQ} einsetzen:

vec{PQ} ~=~ (matrix{3}{1}{{3 - 200 lambda} {-4 + 500 mu + 100 lambda} {1 - 100 mu}}) = (matrix{3}{1}{1/21 2/21 10/21}) ~=~ 1/21 (matrix{3}{1}{1 2 10})

Der gesuchte Abstand ist die Länge des Vektors vec{PQ}:

delim{|}{vec{PQ}}{|}~=~ 1/21 delim{|}{(matrix{3}{1}{1 2 10})}{|} ~=~ 1/21 sqrt{1^2 + 2^2 + 10^2} ~=~ 1/21 sqrt{105} approx~0,488

Bestimmen der Koordinaten von P und Q

Zum Bestimmen des Abstands waren die eigentlichen Koordinaten der Fußpunkte P und Q unwichtig, für die weiteren Berechnungen der Aufgabe müssen sie nun bestimmt werden.

vec{p} ~=~ (matrix{3}{1}{0 4 2}) ~+~ lambda (matrix{3}{1}{200 {-100} 0})~=~(matrix{3}{1}{0 4 2}) ~+~ 3/2100 (matrix{3}{1}{200 {-100} 0}) ~=~(matrix{3}{1}{62/21 53/21 2})~=~ 1/21 (matrix{3}{1}{62 53 42})

vec{q} ~=~ (matrix{3}{1}{3 0 3}) ~+~ mu (matrix{3}{1}{0 500 {-100}}) ~=~ (matrix{3}{1}{3 0 3}) ~+~ 11/2100 (matrix{3}{1}{0 500 {-100}}) ~=~ (matrix{3}{1}{3 55/21 52/21}) ~=~ 1/21 (matrix{3}{1}{63 55 52})

Wann werden P und Q durch die Flugzeuge erreicht?

Jetzt heißt es praktisch denken ;-) - wie kommt man vom Start (Ort zum Zeitpunkt 0) zum gewünschten Punkt?

Mathematisch: Stützvektor + lambda (bzw. mu) mal Richtungsvektor

Also geben lambda bzw. mu die notwendigen Flugzeiten an, d.h. das Sportflugzeug braucht ca. 0,0148 h, das Militärflugzeug ca. 0,0052 h. Umgerechnet in Sekunden benötigt das Sportflugzeug also ca. 53 s, das Militärflugzeug ca. 19 s.

Die kleinste Entfernung der Flugzeuge

:?: Warum ist diese Frage durch Bestimmung des Abstands der beiden Geraden noch nicht gelöst?

:!: Weil die Flugzeuge zu unterschiedlichen Zeiten an P bzw. Q sind (lambda <> mu).

Der zu bestimmende Abstand muss also größer als der schon berechnete Abstand der Flugrouten sein. Außerdem muss jetzt lambda ~=~ mu gelten, damit die Flugzeuge zur selben Zeit am betrachteten Ort sind. Daher wird für den Faktor nun tau verwendet.

Abstand der Flugzeuge: delim{|}{vec{m}~-~vec{s}}{|}, dabei steht vec{m} wieder für das Militärflugzeug, vec{s} für das Sportflugzeug.

vec{m} ~-~ vec{s} ~=~ [(matrix{3}{1}{3 0 3}) ~+~ tau (matrix{3}{1}{0 500 {-100}})] ~-~ [(matrix{3}{1}{0 4 2}) ~+~ tau (matrix{3}{1}{200 {-100} 0})]


~~~~=~ (matrix{3}{1}{3 {-4} 1}) ~+~ tau (matrix{3}{1}{{-200} 600 {-100}}) ~=~ (matrix{3}{1}{{3-200 tau} {-4 + 600 tau} {1 - 100 tau}})

delim{|}{vec{m}~-~vec{s}}{|} ~=~ sqrt{(3-200 tau)^2 + (-4+600 tau)^2 + (1 - 100 tau)^2} ~=~sqrt{26 - 6200 tau + 410000 tau^2}

Der Abstand ist am kleinsten, wenn der Ausdruck unter der Wurzel am kleinsten ist - und das wäre ja gerade das Minimum dieser quadratischen Funktion d(tau) ~=~ 410000 tau^2 - 6200 tau + 26. Das berechnen wir mit der ersten Ableitung:

d prime (tau) ~=~ 820000 tau - 6200 ~=~ 0 ~~~ doubleleftright ~~~ tau ~=~ 31/4100 approx~ 0,0076

windschiefe Gerade

Setzt man diesen Wert in die Abstandsfunktion ein, so erhält man als minimalen Abstand der beiden Flugzeuge ca. 1,6 km (in grün gezeichnet) - zur Erinnerung: der geringste Abstand der Flugrouten betrug ca. 0,488 km (in rot gezeichnet).

, ,
1)
Buch: S. 237 ff
2)
Buch S. 251 ff
3)
Buch S. 251 ff, insbesondere S. 255 ff
4)
Abbildung im Buch auf S. 255
5)
S. 258, Aufgabe 7
schule/ma/regelns2/lag/abstand.txt · Zuletzt geändert: 2018/06/09 11:58 von ahrens
Zeige QuelltextÄltere Versionen
Medien-ManagerNach oben
CC Attribution-Noncommercial-Share Alike 4.0 International
Driven by DokuWiki Recent changes RSS feed Valid CSS Valid XHTML 1.0