Mit Wurzeln umgehen

Die Wurzel aus einer Zahl ist die Zahl, die, mit sich selbst multipliziert, wieder die ursprüngliche Zahl ergibt.

Beispiele:

denn denn

denn $sqrt{a^2} ~=~ a ~~~$ denn

Damit sollte auch klar sein, dass man aus negativen Zahlen keine Wurzeln ziehen kann, weil Quadratzahlen immer positiv sind.

Wurzeln annähern

Bei Quadratzahlen und Brüchen aus Quadratzahlen kann man also problemlos die Wurzeln bestimmen - bei allen anderen Zahlen kann auch der Taschenrechner nur Näherungslösungen angeben.

Beispiele:

denn

Für exakte Lösungen sollte man also mit rechnen, für in der Praxis ausreichende Näherungslösungen reichen die vier Nachkommastellen des ersten Beispiels.

Wurzeln genau zeichnen

Auch wenn man eine Strecke mit der Länge nie genau abmessen kann ist doch möglich, so eine Strecke exakt zu zeichnen.

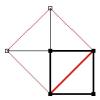
Wenn man annimmt, dass die Seiten des schwarzen Quadrats die Länge 1 haben, dann hat das schwarze Quadrat den Flächeninhalt 1.

Das schwarze Quadrat besteht aus 2 rechtwinkligen Dreiecken mit den Kathetenlängen 1. Das rote Quadrat, dessen Quadratseite die Diagonale im schwarzen Quadrat ist, besteht aus 4 solchen Dreiecken. Also ist der Flächeninhalt des roten Quadrates genau doppelt so groß wie der des schwarzen Quadrates - der Flächeninhalt des roten Quadrates ist also 2.

Bei einem Quadrat mit dem Flächeninhalt 2 muss die Länge der Quadratseiten dann also sein. Damit lässt sich eine Strecke mit einer irrationalen Länge zeichnen, wie hier die Diagonale im Quadrat.

Wurzelterme vereinfachen

Hat das schwarze Quadrat die Seitenlänge , so hat es den Flächeninhalt . Das rote Quadrat hat dann den Flächeninhalt . Die Seitenlänge eines Quadrates mit den Flächeninhalt ist dann gleich $sqrt{2a^2} ~=~ sqrt{2} ~*~ sqrt{a^2} ~=~ a sqrt{2}$ .