Inhaltsverzeichnis
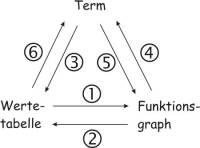
Funktionsterm, Wertetabelle und Funktionsgraph
Die drei Darstellungsformen einer Funktion lassen sich (mehr oder weniger) einfach ineinander umwandeln.
(1) Wertetabelle in Graph
Die Wertetabelle gibt die Koordinaten der Punkte (x|y) an. Diese müssen nur in ein Koordinatensystem eingetragen werden um den Funktionsgraph zu erhalten.
(2) Aus dem Graphen die Wertetabelle ermitteln
Aus der Zeichnung die Koordinaten verschiedener Punkte ablesen, in eine Tabelle eintragen.
(3) Mit Hilfe des Terms eine Wertetabelle anlegen
Werte für x ausdenken, damit die Werte für y berechnen und in die Tabelle eintragen (ausführliche Beschreibung im Regelheft).
(4) Aus Graph den Term bestimmen
Zunächst einmal sollte man anhand des Graphen bestimmen, um was für eine Funktion es sich handelt. Für alle Funktionstypen sollte dann der Schnittpunkt mit der y-Achse abgelesen werden. Häufig sind auch die Schnittpunkte mit der x-Achse hilfreich.
Um den genauen Term zu bestimmen, muss man dann etwas rechnen.
Lineare Funktion
Graph: Gerade
Term: y = mx + b
Der Achsenabschnitt b liest man ab (Schnittpunkt der Gerade mit der y-Achse).
Die Steigung m bestimmt man mit einem Steigungsdreieck.
(5) Aus dem Term den Funktionsgraph erstellen
Für alle Funktionen gilt, dass man natürlich zuerst mit Hilfe des Terms eine Wertetabelle anlegen kann (3) und die erhaltenen Punkte dann in ein Koordinatensystem eintragen kann (1).
Bei manchen Funktionen kann man aber auch schneller zum Ziel kommen.
Lineare Funktion
Als erstes trägt man den Achsenabschnitt als Punkt mit den Koordinaten (0|b) ein. Dann zeichnet man von diesem Punkt aus ein Steigungsdreieck: Man zeichnet eine Einheit parallel zur x-Achse nach rechts und von dort senkrecht um den Wert der Steigung nach oben (wenn die Steigung positiv ist) oder nach unten (wenn sie negativ ist).
Damit hat man einen zweiten Punkt. Durch diesen Punkt und den Achsenabschnitt ist die Gerade festgelegt und kann gezeichnet werden.
Nachtrag: Wenn die Steigung als Bruch angegeben ist, z.B. m = , kann man soviele Einheiten wie der Nenner angibt nach rechts zeichnen (hier: 3) und dann soviele Einheiten wie der Zähler angibt nach unten oder oben (hier: 5 nach oben).
(6) Aus der Wertetabelle den Term ermitteln
Das wird nicht immer gehen - Voraussetzung ist eine recht umfangreiche Wertetabelle, je nach Funktionstyp. Hilfreich ist sicher, zunächst aus den gegebenen Punkten einen Graph zu zeichnen, damit weiß man dann meistens um was für eine Funktion es sich handelt. Dann kann man auch weiter wie in (4) vorgehen.
Lineare Funktion
Wenn man weiß, dass es sich um eine lineare Funktion handelt, reichen zwei Punkte aus, um den Term zu bestimmen.
Als erstes berechnet man die Steigung mit .
Dann setzt man in den Term die berechnete Steigung
und die Koordinaten
und
eines der gegebenen Punkte ein. Die Gleichung kann man dann nach
auflösen und erhält damit den Wert des Achsenabschnitts.
Beispiel:
|
|
|
Damit lautet der gesuchte Funktionsterm hier im Beispiel .