Inhaltsverzeichnis
Funktionen und Funktionsgraphen
Eine Funktion ist eine Zuordnung, die jeder möglichen Ausgangsgröße genau eine zugeordnete Größe zuordnet.
Wir nennen die Ausgangsgröße üblicherweise x und die zugeordnete Größe y.
Alle Zahlen, die für x gewählt werden können, bilden zusammen den Definitionsbereich einer Funktion.
Alle Zahlen, die für y möglich sind, bilden zusammen den Wertebereich der Funktion.
Darstellung
Funktionen können als
- Diagramm
- Tabelle
- Term
- oder Text (Wortvorschrift)
dargestellt werden.
1. Beispiel
Text: Die Versandkosten betragen einmalig 3,90 € und für jeden weiteren Artikel 1 € zusätzlich.
Term:
Hier steht y für die Versandkosten insgesamt und x für die Anzahl der zusätzlichen Artikel.
Tabelle: (aus Platzgründen in Zeilenform)
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| y = 3,9 + x | 3,9 | 4,9 | 5,9 | 6,9 | 7,9 | 8,9 | 9,9 | 10,9 |
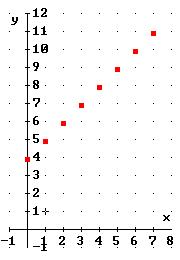
Diagramm: Da die Ausgangsgröße x für „Anzahl zusätzlicher Artikel“ steht, und die nur ganzzahlig sein können, dürfen in diesem Fall die Punkte nicht verbunden werden.
2. Beispiel
Text: Auf einem Sparbuch werden 42 € zusammen mit den anfallenden Zinsen mit 1% verzinst.
Term:
Hier steht y für den Endbetrag und x für die Jahre, die das Geld auf dem Sparbuch liegt.
Tabelle:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 50 |
|---|---|---|---|---|---|---|---|
| y | 42 | 42,42 | 42,84 | 43,27 | 43,71 | 44,14 | 69,07 |
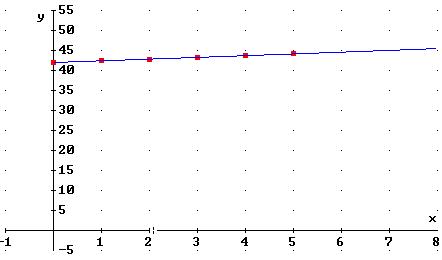
Diagramm:
Begriffe
Funktionen haben einen Funktionsnamen, z.B. , eine Funktionsvariable, (normalerweise)
und einen Funktionswert, (normalerweise)
.
Man schreibt:
Und sagt: f von x ist gleich y, oder f hat an der Stelle x den Wert y
Beispiel
f( 1 ) = 0 beschreibt den Punkt mit den Koordinaten (1|0)
f( 8 ) = 3 beschreibt den Punkt mit den Koordinaten (8|3)
Besondere Funktionen und ihre Graphen
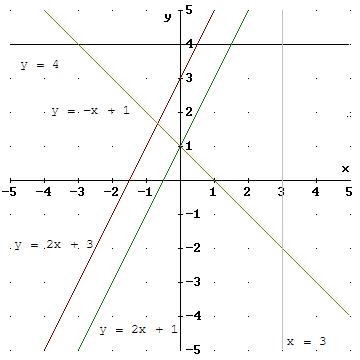
Lineare Funktionen - Geraden
Man nennt den Graph einer linearen Funktion Gerade.
Jede Lineare Funktion hat einen Funktionsterm der folgenden Form (mit f(x) = y):
Der Faktor m gibt an, wie steil die Gerade ist. Man nennt diesen Faktor daher Steigung.
Der Summand b gibt an, wo die Gerade die y-Achse schneidet, da f(0) = b gilt. Man nennt diesen Summanden daher Achsenabschnitt.
x und y sind die Koordinaten der Punkte der Gerade.
Lineare Funktionen mit identischem Achsenabschnitt haben den Punkt (0|b) gemeinsam - die Geraden schneiden sich also in diesem Punkt.
Lineare Funktionen mit identischer Steigung verlaufen Parallel.
Eine Gerade mit der Steigung m = 0 verläuft parallel zur x-Achse und hat dann z.B. einen Funktionsterm wie y = 4.
Eine Gerade, die parallel zur y-Achse verläuft, stellt keine Funktion dar, da hier einem x-Wert beliebig viele y-Werte zugeordnet werden. Aber auch solch eine Gerade kann mit einem Term beschrieben werden. So hat z.B. eine Parallele zur y-Achse, die die x-Achse an der Stelle x = 3 schneidet, den Term x = 3.