Vektoren und Geraden

Zu folgenden Begriffen sollte euch noch etwas einfallen:

• Darstellung eines Vektors (üblicherweise im Bild als Pfeil, im mathematischen Ausdruck in Form der untereinanderstehenden Koordinaten)
• Unterschied zwischen Vektor und Strecke (Vektoren haben eine Richtung, die genaue Lage von Anfangs- und Endpunkt ist zunächst egal)
• skalare Multiplikation (Verlängerung eines Vektors)
• Vektoraddition und -subtraktion
• Berechnung der Länge eines Vektors (Pythagoras)

Beispiele für Vektoren sind z.B. $\vec{a} = \left( \begin{array}{c}4\\ 2\\ 3\end{array} \right)$ oder $\vec{b} = \left( \begin{array}{c}2\\ 6\\ 3\end{array} \right)$ oder $\vec{c} = \left( \begin{array}{c}5\\ 7\\ 4\end{array} \right)$

Legt man den Anfangspunkt dieser Vektoren in den Ursprung, so zeigen diese Vektoren auf den Punkt mit den angegebenen Koordinaten, sie sind dann also Ortsvektoren.

Für $A(4|2|3)$ ist also $\vec{a} = \vec{OA}= \left( \begin{array}{c}4\\ 2\\ 3\end{array} \right)$ der Ortsvektor.

Will man diese Vektoren zeichnen, so benötigt man ein dreidimensionales Koordinatensystem. Die in der Papierebene liegenden Achsen werden jetzt als y-Achse (rechts) und z-Achse (hoch) benannt, die x-Achse steht dann in Wirklichkeit senkrecht zur Papierebene. Wie im Schrägbild zeichnet man die x-Achse daher im 45°-Winkel zur y- bzw. z-Achse. Außerdem muss die Einheit im Vergleich zur y- und zur z-Achse halbiert werden. Um das Zeichnen zu vereinfachen wählt man auf dem Kästchenpapier zwei Kästchen als Einheit auf der y- und der z-Achse, eine Kästchendiagonale auf der x-Achse.

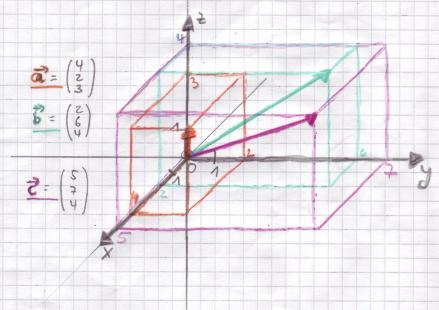
Um den räumlichen Eindruck zu erhöhen, wurden die Vektoren hier als Raumdiagonalen von Quadern gezeichnet, deren eine Ecke im Ursprung liegt.

Wie in der ebenen Geometrie auch bilden Ursprungsgeraden eine besondere Unterklasse der Geraden. Alle diese Geraden enthalten den Ursprung des Koordinatensystems, O, als Punkt. Jeder beliebige Ortsvektor (diese haben immer den Ursprung als Startpunkt) kann also die Richtung einer bestimmten Gerade festlegen.

Um nun aus einem bestimmten Vektor eine Gerade zu erzeugen, muss man diesen Vektor beliebig verlängern oder verkürzen können (in beide Richtungen), um jeden Punkt der Gerade zu erreichen. Ein Vektor wird durch skalare Multiplikation verlängert oder verkürzt, daher wird eine Ursprungsgerade in Vektorschreibweise z.B. durch den folgenden Ausdruck beschrieben:

\[\vec{g}= k \cdot \vec{a} = k \cdot \left( \begin{array}{c}4\\ 2\\ 3\end{array} \right)\]

Nimmt der skalare Faktor k Werte größer als 1 an, so liegt der Punkt auf der Gerade außerhalb des Vektors, liegen die Werte zwischen 0 und 1 so liegen die Punkte auf dem Vektor. Hat k einen Wert kleiner als 0, so liegen die Punkte auf der anderen Seite des Ursprungs, mit k = 0 wird der Ursprung erreicht.

Durch die Vektorschreibweise kann jeder, wie auch in der allgemeinen Form einer Gerade in der Ebene, ein- und dieselbe Gerade unterschiedlich ausdrücken.

Zum Aufstellen der Geradengleichung muss man zwei Fälle unterscheiden:

1. Ein Ortsvektor $\vec{a}$ und ein Richtungsvektor $\vec{r}$ sind gegeben: Dann lautet die Geradengleichung $\vec{x} = \vec{a} + \lambda \, \vec{r}$
   
2. Zwei Ortsvektoren, $\vec{a}$ und $vec{b}, sind gegeben: Dann hat man (solange keine weiteren Bedingungen genannt sind) für die Geradengleichung vier gleichwertige Möglichkeiten,
   • $\vec{x} = \vec{a} + \lambda \, (\vec{b} - \vec{a})$
   • $\vec{x} = \vec{a} + \lambda \, (\vec{a} - \vec{b})$
   • $\vec{x} = \vec{b} + \lambda \, (\vec{b} - \vec{a})$
   • $\vec{x} = \vec{b} + \lambda \, (\vec{a} - \vec{b})$

Bei einer Ursprungsgerade liegt der Punkt $O(0|0|0)$ auf der Gerade, hier könnte man dann den Ortsvektor durch den Nullvektor, $\vec{o}$, ersetzen und damit auch einfach weglassen.

Drei Vektoren können, wenn einer das Vielfache eines der anderen ist (also z.B. $\vec{a} =k \, \vec{b}$, wieder genau eine Gerade beschreiben - die Vektoren, die Vielfache voneinander sind, müssen dann die Richtung der Gerade angeben.

Drei Vektoren können aber auch eine Ebene festlegen.

Wenn die Summe oder die Differenz von zwei Vektoren den dritten Vektor ergibt, so liegen die drei Vektoren in einer Ebene (diese Vektoren bilden also die Seiten eines Dreiecks).

Zwei Vektoren liegen immer in einer Ebene, der dritte Vektor gibt dann einen Punkt in der Ebene an und legt dadurch die Lage der Ebene im Raum fest. Eine allgemeine Form der Ebenengleichung sieht daher so aus:

\[E:~\vec{x} = \vec{a} + \lambda \vec{u} + \mu \vec{v}\]

Den Ortsvektor $\vec{a}$ zum Ebenenpunkt nennt man dann auch Stützvektor, die in der Ebene liegenden Vektoren $\vec{u}$ und $\vec{v}$ Spannvektoren.

Drei Ortsvektoren geben drei Punkte im Raum an - drei Punkte liegen immer in einer Ebene. Zur Bestimmung der Ebenengleichung geht man hier wie bei der Geradengleichung vor: Einer der drei Vektoren, z.B. $\vec{a}$, wird als Stützvektor gewählt, mit den anderen Ortsvektoren $\vec{b}$\, $\vec{c}$ und dem Stützvektor $\vec{a}$ berechnet man dann die Spannvektoren.

\[E:~ \vec{x} = \vec{a} + \lambda (\vec{b} - \vec{a}) + \mu (\vec{c} - \vec{a})\]